MPC regulador con filtro de Kalman

Comentarios

Código fuente

También disponible en:

English

Tabla de Contenido

Control Predictivo basado en Modelo (MPC - Model Predictive Control) tipo regulador sin restricciones con filtro de Kalman

Lo siguiente presenta una simulación de Control Predictivo basado en Modelo Cuadrático Lineal (LQ-MPC - Linear Quadractic-Model Predictive Control) no restringido usando el kernel de Matlab para Jupyter Notebook. Los archivos de código se pueden usar en Matlab de forma nativa.

Requisitos previos

  • Conocimiento en teoría de sistemas de control.
  • Teoría de optimización cuadrática convexa.
  • Jupyter Notebook con kernel de Matlab.
  • Matlab.

Antecedentes

MPC es una estrategia de control basada en la optimización que resuelve un problema de Horizonte Finito Lineal Cuadrático (FH-LQ - Finite Horizon Linear Quadratic) sujeto a restricciones. Se utiliza un modelo de estados predecidos basados en la dinámica del sistema para minimizar una función objetivo que satisface las restricciones dados los estados actuales. La solución obtenida es una secuencia de controles de lazo abierto, de los cuales solo se implementa el primero en el sistema, induciendo retroalimentación. El resto de la secuencia se descarta y el proceso se repite para el siguiente tiempo de muestreo, este método se llama a menudo principio de Horizonte en Retroceso (RH - Receding Horizon). Las ventajas del MPC sobre otras estrategias de control son el manejo de restricciones y no linealidades del sistema.

MPC sin restricciones

MPCu
Fig.1 - MPC sin restricciones

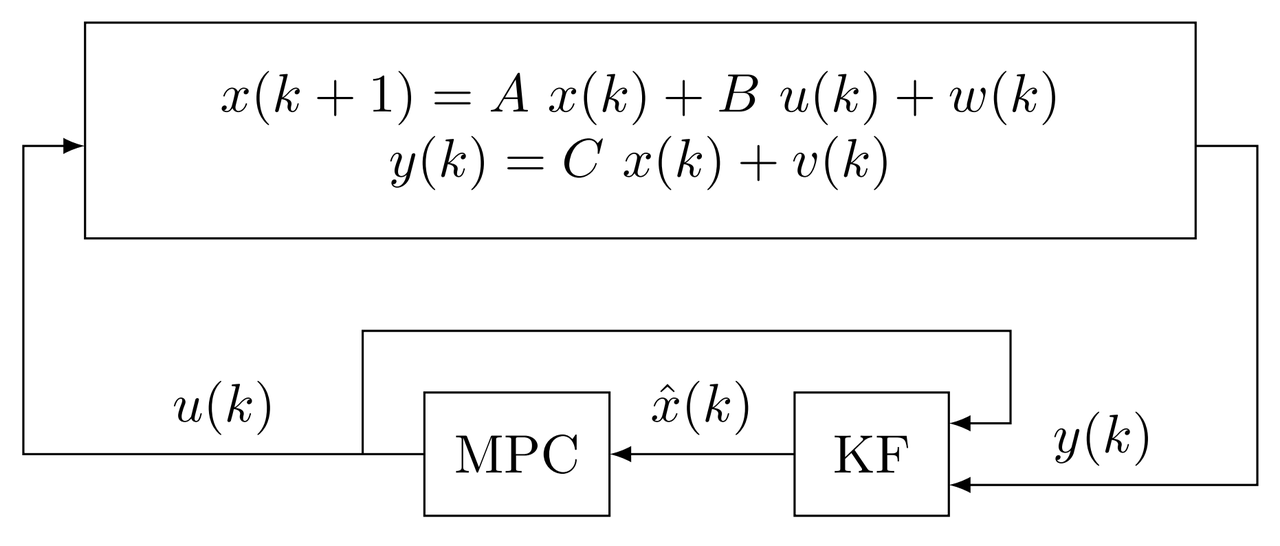
Considere el siguiente sistema en espacio de estados LTI en tiempo discreto

\begin{equation*} \begin{aligned} x(k+1) &= A~x(k)+B~u(k)+w(k)\\ y(k) &= C~x(k)+v(k),\quad k=0,1,2,\dots \end{aligned} \end{equation*}

donde $x\in\mathbb{R}^n$, $u\in\mathbb{R}^m$, y $y\in\mathbb{R}^p$, son los vectores de estados, entrada, y salida respectivamente. $A,~B,~C$ son las matrices de estados, entrada y salida. $A,~B,~C$ son conocidas, no hay incertidumbres en el modelo, perturbaciones ni ruido. $x(k)$ está disponible en cada tiempo de muestreo $k$. El ruido del proceso es $w(k)\sim \mathcal{N}(0,Q_w)$ con covarianza $Q_w$, el ruido de medición es $v(k)\sim \mathcal{N}(0,R_v)$ con covarianza $R_v$, ambos son no correlacionados, y están en forma de ruido blanco gaussiano aditivo (AWGN).

Formulación del problema

El objetivo es regular $x\rightarrow 0$ a medida que $k\rightarrow \infty$ mientras se minimiza la siguiente función de costo

\begin{align*}\tag{1} J_N(x(k),\mathbf{u}(k)) &= \sum_{j=0}^{N-1} \left( \|x(k+j|k)\|^2_Q + \|u(k+j|k)\|^2_R \right) + \|x(k+N|k)\|^2_P \\ &= \sum_{j=0}^{N-1} (x^\intercal(k+j|k)~Q~x(k+j|k)+ u^\intercal(k+j|k)~R~u(k+j|k) ) + x^\intercal(k+N|k)~P~x(k+N|k) \end{align*}

sujeto a,

\begin{align*}\tag{2} x(k+1+j|k) &= A~x(k+j|k)+B~u(k+j|k) \\ x(k|k) &= x(k) \end{align*}

para $ j=0,1,2,\dots,N-1$.

Donde $Q\in\mathbb{R}^{n\times n}$ y $R\in\mathbb{R}^{m\times m}$ son las matrices de penalización de estado e input respectivamente. $P\in\mathbb{R}^{n\times n}$ es la matriz de costo terminal, $N \in\mathbb{N}$ es la longitud del horizonte, $k$ es el tiempo de muestreo, y $(k+j|k)$ se puede definir como el siguiente valor $(k+j)$ dado $k$.

Con la función de valor definida como \begin{align*} J^*_N(x(k),\mathbf{u}(k)) &= \min_{u(k)}~ J_N(x(k),\mathbf{u}(k)) \end{align*} la secuencia de control óptima es \begin{equation*} \begin{aligned} \mathbf{u}^*(k) &= \mathrm{arg}\min_{u(k)}~ J^*_N(x(k),\mathbf{u}(k))\\ &= \left\{ u^*(k|k),u^*(k+1|k),\dots,u^*(k+N-1|k) \right\} \end{aligned} \end{equation*}

El enfoque del Problema Cuadrático (QP - Quadratic Problem)

Está dividido en cuatro secciones

  • Predicción
  • Optimización
  • Horizonte Recesivo
  • Estabilidad

Predicción: Restricción de Igualdad Predecida

Estableciendo $x(k)=x(k|k)$ y $u(k)=u(k|k)$, y aplicando el modelo recursivamente

\begin{align*} x(k+1|k) &= A~x(k)+B~u(k) \\ x(k+2|k) &= A~x(k+1|k)+B~u(k+1|k) \\ &= A^2~x(k)+AB~u(k|k)+B~u(k+1|k) \\ \vdots \hspace{2em} &= \hspace{3em} \vdots \\ x(k+N|k) &= A~x(k+N-1|k)+B~u(k+N-1|k) \\ &= A^N~x(k)+A^{N-1}B~u(k|k)+\dots+B~u(k+N-1|k) \end{align*}

agrupando

\begin{align*} {\underbrace{ \begin{bmatrix} x(k+1|k) \\ x(k+2|k) \\ \vdots \\ x(k+N|k) \end{bmatrix}}_{\mathbf{x}(k)} } = {\underbrace{ \begin{bmatrix} A \\ A^2 \\ \vdots \\ A^N \end{bmatrix}}_{F} } + {\underbrace{ \begin{bmatrix} B & 0 & \dots & 0 \\ AB & B & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ A^{N-1}B & A^{N-2}B & \dots & B \end{bmatrix}}_{G} } {\underbrace{ \begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix}}_{\mathbf{u}(k)} } \end{align*}

la restricción de igualdad predecidahe predicted es

\begin{equation}\tag{3} \mathbf{x}(k) = F~x(k)+G~\mathbf{u}(k) \end{equation}

donde $\mathbf{x}(k)$ y $\mathbf{u}(k)$ son los estados, predicciones de entradad sobre todos los pasos $j=0,1,2,\dots,N$.

Predicción: Reescribiendo la función de costo

Reescribiendo la función de costo tal que

\begin{aligned} x^\intercal(k|k)~Q~x(k|k) &+ \begin{bmatrix} x(k+1|k) \\ x(k+2|k) \\ \vdots\\ x(k+N|k) \\ \end{bmatrix}^\intercal {\underbrace{ \begin{bmatrix} Q & 0 & \dots & 0 \\ 0 & Q & \ddots & \vdots \\ \vdots & \ddots & Q & 0 \\ 0 & \dots & 0 & P \end{bmatrix}}_{\tilde{Q}} } \begin{bmatrix} x(k+1|k) \\ x(k+2|k) \\ \vdots\\ x(k+N|k) \\ \end{bmatrix} \\ &+ \begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix}^\intercal {\underbrace{ \begin{bmatrix} R & 0 & \dots & 0 \\ 0 & R & \ddots & \vdots \\ \vdots & \ddots & R & 0 \\ 0 & \dots & 0 & R \end{bmatrix}}_{\tilde{R}} } \begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix} \end{aligned}

Entonces, con $x(k|k)=x(k)$ ahora el problema es minimizar

\begin{align}\tag{4} J_N(x(k),\mathbf{u}(k)) &= x^\intercal(k)~Q~x(k) + \mathbf{x}^\intercal(k)~\tilde{Q}~\mathbf{x}(k) + \mathbf{u}^\intercal(k)~\tilde{R}~\mathbf{u}(k) \end{align}

sujeto a,

\begin{align*} \mathbf{x}(k) &= F~x(k)+G~\mathbf{u}(k) \end{align*}

Substituting the predicted equality constraint (3) into the Cost Function (4)

Omitting $(k)$ only for the algebraic operations, \begin{align*} J_N(x(k),\mathbf{u}(k)) &= x^\intercal(k) Q x(k) + ( F x(k)+G \mathbf{u}(k) )^\intercal \tilde{Q} ( F x(k)+G \mathbf{u}(k) ) + \mathbf{u}^\intercal(k)~\tilde{R} \mathbf{u}(k) \\ &= x^\intercal Q x + [(F x)^\intercal+(G \mathbf{u})^\intercal] \tilde{Q} (F x+G \mathbf{u}) + \mathbf{u}^\intercal \tilde{R} \mathbf{u} \\ &= x^\intercal Q x + (F x)^\intercal \tilde{Q} F x + (F x)^\intercal \tilde{Q} G \mathbf{u} + (G \mathbf{u})^\intercal \tilde{Q} F x + (G \mathbf{u})^\intercal \tilde{Q} G \mathbf{u} + \mathbf{u}^\intercal~\tilde{R} \mathbf{u}\\ &= \underbrace{x^\intercal Q x + x^\intercal F^\intercal \tilde{Q} F x} + \underbrace{x^\intercal F^\intercal \tilde{Q} G \mathbf{u} + \mathbf{u}^\intercal G^\intercal \tilde{Q} F x} + \underbrace{\mathbf{u}^\intercal G^\intercal \tilde{Q} G \mathbf{u} + \mathbf{u}^\intercal \tilde{R} \mathbf{u}}\\ &= x^\intercal(Q+F^\intercal \tilde{Q} F)x \quad \!\!+ \quad 2 \mathbf{u}^\intercal G^\intercal \tilde{Q} F x \qquad\quad+ \mathbf{u}^\intercal (G^\intercal \tilde{Q} G+\tilde{R})\mathbf{u}\\ &= x^\intercal(Q+F^\intercal \tilde{Q} F)x + (2 G^\intercal \tilde{Q} F x)^\intercal \mathbf{u} + \mathbf{u}^\intercal (G^\intercal \tilde{Q} G+\tilde{R})\mathbf{u}\\ &= x^\intercal\underbrace{(Q+F^\intercal \tilde{Q} F)}_M x + (\underbrace{2 G^\intercal \tilde{Q} F}_L x)^\intercal \mathbf{u} + \frac{1}{2}\left[\mathbf{u}^\intercal \underbrace{2(G^\intercal \tilde{Q} G+\tilde{R})}_H \mathbf{u}\right]\\ &= \frac{1}{2}\mathbf{u}(k)^\intercal~H~\mathbf{u}(k)+\underbrace{(L~x(k))^\intercal}_{c^\intercal}~\mathbf{u}(k)+\underbrace{x(k)^\intercal~M~x(k)}_\alpha \end{align*}

we obtain the cost function in compact form...

Función de costo in forma quadrática compacta

\begin{align}\tag{5} J_N(x(k),\mathbf{u}(k)) &= \frac{1}{2} \mathbf{u}(k)^\intercal~H~\mathbf{u}(k)+c^\intercal~\mathbf{u}(k)+\alpha \end{align}

donde \begin{align*} H&=2(G^\intercal\tilde{Q}G+\tilde{R})\\ c&=L~x(k) \\ L&=2G^\intercal\tilde{Q}F\\ \alpha&=x^\intercal(k)~M~x(k) \\ M&=Q+F^\intercal\tilde{Q}F \end{align*}

Optimización: Solución explícita de $J_N(x(k)$

Minimizando por gradiente y resolviendo para $\mathbf{u}^*(k)$,

\begin{align*} J^*_N(x(k),\mathbf{u}(k)) &= \min_{\mathbf{u}(k)}~\frac{1}{2} \mathbf{u}(k)^\intercal~H~\mathbf{u}(k)+c^\intercal~\mathbf{u}+\alpha \\ \nabla_\mathbf{u}~J^*_N(x(k),\mathbf{u}(k)) &= 0 \\ H~\mathbf{u}^*(k)+c &= 0 \\ \mathbf{u}^*(k) &= -H^{-1}~c \end{align*}

la solución óptima resulta en

\begin{align}\tag{6} \mathbf{u}^*(k) &= -H^{-1}~L~x(k) \end{align}

donde $Q\succeq,~P\succeq 0$ son convexos semidefinidos positivos, y $R\succ 0$ es convexo definido, tal que $H\succ 0$. La solución óptima $\mathbf{u}^*(k)$ para cualquier $x(k)$ es única si $H\succ 0$ es invertible.

Horizonte en Retroceso

Aplicar el principio de Horizonte en Retroceso significa que solo se aplica al sistema real el $\textbf{primer}$ control de entrada del vector $\mathbf{u}^*(k)$. Es decir

\begin{align*} \begin{bmatrix} u^*(k) \\ u^*(k+1) \\ \vdots \\ u^*(k+N-1) \end{bmatrix} &= \begin{bmatrix} I & 0 & 0 & \dots & 0 \\ 0 & I & 0 & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & I \end{bmatrix} (-H^{-1}~L)x(k) \end{align*}\begin{align*}\tag{7} u^*(k) &= K_N~x(k) \\ K_N &= [I \quad 0 \quad 0 \quad \dots \quad 0](-H^{-1}~L) \end{align*}

Observa que $u^*(k)$ es una ley de control lineal explícita e invariante en el tiempo porque $H$ y $L$ no dependen de $x(k)$.

Estabilidad

Para garantizar la estabilidad de circuito cerrado del sistema, utilizamos el enfoque MPC de modo dual, donde la matriz de costo terminal $P$ se calcula para imitar un horizonte infinito tal que \begin{align*} x^\intercal(k+N|k)~P~x(k+N|k) &= \sum_{j=N}^{\infty} (x^\intercal(k+j|k)~Q~x(k+j|k)+ u^\intercal(k+j|k)~R~u(k+j|k) ) \end{align*}

Usando la siguientes condiciones

  • $(A,B)$ is stabilizable
  • $Q\succeq0,~R\succ0$
  • $(Q^{1/2},A)$ is observable

El enfoque MPC de modo dual establece que hay un $P\succ0$ único que satisface la ecuación de Lyapunov para alguna ganancia estabilizadora $K$ \begin{align}\tag{8} (A+B~K)^\intercal ~P~(A+B~K)-P = -(Q+K^\intercal~R~K) \end{align} donde $K$ es la ley de control del modo-2 que puede tener cualquier valor siempre que $(A+B~K)$ sea estable.

Por lo tanto, la ley de control $u^*(k)$ se estabiliza asintóticamente. Además, $P$ modifica solo $\tilde{Q}$, lo que significa que la solución óptima sigue siendo explícita.

El modo-2 se usa solo para la estabilidad y el rendimiento, no se aplica a la planta. Si $K=K_\infty$, donde $K_\infty$ es un control LQ de horizonte infinito, la ley de control $u^*(k)$ se conoce como LQ-MPC óptima. Por otro lado, si $K\neq K_\infty\rightarrow K_N\neq K_\infty$ se conoce como LQ-MPC subóptimo.

Algorito

drawing

Ejemplo

Apliquemos el regulador MPC sin restricciones en un sistema de Fase no mínima inestable,

\begin{align*} Gp(s) = \dfrac{1-s}{(s-2)(s+1)} \end{align*}

en forma de espacio de estados con las siguientes condiciones, \begin{align*} x(k+1) &= \begin{bmatrix} 1.1160 & 0.2110 \\ 0.1055 & 1.0100 \end{bmatrix} x(k)+ \begin{bmatrix} 0.1055\\ 0.0052 \end{bmatrix} u(k)+w(k)\\ y(k) &= \begin{bmatrix} -1 & 1 \end{bmatrix} x(k) + v(k)\\ x(0) & = [1.5 \quad 1]^\intercal\\ Ts &= 0.1, \quad N = 5, \quad k = 100\\ Q &= \begin{bmatrix} 1e2 & 0 \\ 0 & 1e2 \end{bmatrix} ,\quad R = 1\\ w(k) & \sim \mathcal{N}(0,1e^{-4}), \quad v(k) \sim \mathcal{N}(0,1e^{-4}) \end{align*}

Definiciones iniciales

Constantes globales, el sistema y las matrices de penalización. La ganancia de modo-2 se usa para calcular $P$.

In [2]:
% Global constants
clear variables;
x0 = [1.5; 1];  % initial conditions
nk = 100;       % simulation steps
Ts = 0.1;       % sampling time
t = Ts*(0:nk);  % simulation time
N = 5;          % horizon 

% System
% sys = (-s+1)/((s-2)*(s+1));
[Ac,Bc,Cc,Dc] = tf2ss([-1 1],[1 -1 -2]);
Bdc = [0;0]; Ddc = 0;
sysc = ss(Ac,[Bc Bdc],Cc,[Dc Ddc]);

sysd = c2d(sysc,Ts);
A = sysd.A; 
B = sysd.B(:,1); 
Bd = sysd.B(:,2); 
C = sysd.C; 
D = sysd.D(:,1);

% Penalty Cost matrices
Q = [ 1e2   0
      0   1e2];
R = 1;

% Mode-2 gain
K = -dlqr(A,B,Q,R)

% Terminal Cost matrix 
Phi = A+B*K;
S = Q+K'*R*K;
P = dlyap(Phi',S)

K =

   -7.6505   -7.6466


P =

   1.0e+03 *

    0.1870    0.1352
    0.1352    1.1868

Filtro de Kalman

In [3]:
% Stream of process noise and measurement noise (AWGN)
rng default;                % For reproducibility (seed)
mu_Qw = [0, 0];             % mean of the states (mu_x1, mu_x2)
Qw = diag([1e-4, 1e-4]);    % process noise covariance. Qw=diag[sigma_x1^2, sigma_x2^2]
w = mvnrnd(mu_Qw,Qw,nk+1);  % noise input vector
% cov(w)                    % covariance matrix of w
% scatter(w(:,1),w(:,2))

mu_Rv = 0;                  % mean of the measurements
Rv = (1e-4)*eye(1);         % measurement noise covariance. Rv=sigma^2
v = mvnrnd(mu_Rv,Rv,nk+1);  % noise output vector

% KF Steady-State
[kest,LKF,Ps] = kalman(sysd,Qw,Rv);
LKF

LKF =

   -0.8435
   -0.4217

Creación de las restricciones de igualdad predecidas $F$ y $G$

In [4]:
% dimensions
n = size(A,1);
m = size(B,2);

% allocate
F = zeros(n*N,n);
G = zeros(n*N,m*(N-1));

% form row by row
for i = 1:N
    % F
    F(n*(i-1)+(1:n),:) = A^i;

    % G
    % form element by element
    for j = 1:i
        G(n*(i-1)+(1:n),m*(j-1)+(1:m)) = A^(i-j)*B;
    end
end

F
G

F =

    1.1159    0.2110
    0.1055    1.0104
    1.2675    0.4487
    0.2244    1.0431
    1.4617    0.7209
    0.3604    1.1013
    1.7071    1.0368
    0.5184    1.1887
    2.0144    1.4078
    0.7039    1.3104


G =

    0.1055         0         0         0         0
    0.0052         0         0         0         0
    0.1188    0.1055         0         0         0
    0.0164    0.0052         0         0         0
    0.1361    0.1188    0.1055         0         0
    0.0291    0.0164    0.0052         0         0
    0.1580    0.1361    0.1188    0.1055         0
    0.0437    0.0291    0.0164    0.0052         0
    0.1855    0.1580    0.1361    0.1188    0.1055
    0.0609    0.0437    0.0291    0.0164    0.0052

Creación de las matrices de costo predecidas $H$, $L$ y $M$

In [5]:
% get dimensions
n = size(F,2);
N = size(F,1)/n;

% diagonalize Q and R
Qd = kron(eye(N-1),Q);
Qd = blkdiag(Qd,P);
Rd = kron(eye(N),R);

% Hessian
H = 2*G'*Qd*G + 2*Rd;

% Linear term
L = 2*G'*Qd*F

% Constant term
M = F'*Qd*F + Q

% make sure the Hessian is symmetric
H = (H+H')/2

L =

  464.7837  464.6681
  358.3690  358.2880
  266.3348  266.2808
  184.9870  184.9540
  111.0602  111.0433


M =

   1.0e+03 *

    2.6666    2.6143
    2.6143    3.6652


H =

   44.1261   32.4810   24.1394   16.7664   10.0660
   32.4810   28.5940   19.7642   13.7275    8.2415
   24.1394   19.7642   18.1822   11.2395    6.7478
   16.7664   13.7275   11.2395   11.2025    5.5248
   10.0660    8.2415    6.7478    5.5248    6.5236

Obteniendo la ganancia de Horizonte en Retroceso (RH - Receding Horizon)

In [6]:
%% Unconstrained MPC: RH-FH-LQR/LQ-MPC
Ku = -H\L      % solution
KN = Ku(1,:)   % RH-FH gain, first row of the m-row matrix

Ku =

   -7.6505   -7.6466
   -2.8647   -2.8645
   -1.0728   -1.0738
   -0.4018   -0.4032
   -0.1506   -0.1520


KN =

   -7.6505   -7.6466

For loop

In [7]:
% Init
x_mpc_u = x0;
xs_mpc_u = zeros(n,nk+1);
us_mpc_u = zeros(m,nk+1);

for k = 1:nk+1
    xs_mpc_u(:,k) = x_mpc_u;    
    y_mpc_u(k) = C*x_mpc_u + v(k); 
    us_mpc_u(:,k) = KN*x_mpc_u;
    x_mpc_u = A*x_mpc_u+B*us_mpc_u(:,k) + LKF*(y_mpc_u(k)-C*x_mpc_u) + w(k,:)';        
    J_mpc_u(k) = x_mpc_u'*Q*x_mpc_u+us_mpc_u(:,k)'*R*us_mpc_u(:,k);     
end

























Resultados



Entradas de control



La señal de control de entrada $u$ llega a cero relativamente rápido debido al costo de penalización $R=1$. Los valores más altos de $R$ llegan a cero lentamente.













In [8]:



    


% Input 
figure;      
    stairs(t,us_mpc_u,'--','LineWidth',1);           
    ylabel('$u$','Interpreter','Latex');
    xlabel('Time step [s]');
    title('Input');     
    grid on;



    















    















    
































Señales de salidas



La salida $y$ converge alrededor de cero lentamente debido a $R$. Observe que la señal refleja la matriz de observación $C=[-1~1]$.













In [9]:



    


% Output
figure;       
    plot(t,y_mpc_u,'--','LineWidth',1);
    ylabel('$y$','Interpreter','Latex');        
    xlabel('Time step [s]'); 
    title('Output');
    grid on;



    















    















    
































Estados



Los estados comienzan en las condiciones iniciales $x(0)=[1.5~1]^\intercal$, y convergen lentamente a cero.













In [10]:



    


% States
figure;
    plot(t,xs_mpc_u(1,:),'--',t,xs_mpc_u(2,:),'--','LineWidth',1);      
    xlabel('Time step [s]'); 
    ylabel('$x_1,~x_2$','Interpreter','Latex','Fontsize',12); 
    title('States');        
    legend('$x_1~$ MPCu','$x_2~$ MPCu',...
            'Location','southeast',...
            'Interpreter','Latex');
    grid on;



    















    















    
































Diagrama de fase



El diagrama de fases muestra más claramente la condición inicial $x(0)$. Además, muestra la convergencia alrededor de cero para $k \rightarrow \infty$













In [11]:



    


% Phase-plot
figure;
    plot(xs_mpc_u(1,:),xs_mpc_u(2,:),'--x','LineWidth',1);
    xlabel('$x_1$','Interpreter','Latex'); 
    ylabel('$x_2$','Interpreter','Latex');
    title('Phase-plot');
    grid on;



    















    















    
































Valor de costo



El valor de costo $J^*_N(x(k),\mathbf{u}(k))$ indica el comportamiento monótono descendente de la función de costo $J_N(x(k),\mathbf{u}(k))$













In [12]:



    


% Cost Value
figure;
    plot(t, J_mpc_u,'--','LineWidth',1);
    xlabel('Time step [s]');  
    ylabel('$J(k)$','Interpreter','Latex');
    title('Cost Value');
    grid on;



    















    















    
































Referencias



[1] James B. Rawlings and Mayne David Q. Model Predictive Control Theory and Design. Nob Hill Pub, Llc, 2009. ISBN: 9780975937709.


[2] Jan Maciejowski. Predictive Control with Constraints. Prentice Hall, 2000. ISBN: 978-0201398236.








    

    
Comentarios

        
    
        

        
    Comments powered by Disqus